Promises: Using Promises To Evaluate Agent Reputation – Part 3

This is the third text in a series about how to make reputation of an agent a function of promises an agent makes, and the outcome of these promises. The text presents a framework in which reputation is a function of promises between agents, and relative to Part 2, here, the probability that an agent will fulfil a promise it made is positively correlated with that agent’s reputation, or past performance with promises it made. Same as the frameworks in Parts 1 and 2, the framework described in this text can be used to create a reputation mechanism to use in decision processes, in multi agent systems, and in general, in situations in which there are repeated interactions and agents depend on each other to realize their goals. A minor difference relative to frameworks in Parts 1 and 2, the notation here is now in plan text, not Latex.

This text is part of the series on decision governance. Decision Governance is concerned with how to improve the quality of decisions by changing the context, process, data, and tools (including AI) used to make decisions. Understanding decision governance empowers decision makers and decision stakeholders to improve how they make decisions with others. Start with “What is Decision Governance?” and find all texts on decision governance here.

Framework Description

The starting set of rules are from Reputation Framework 1. A change is made to clarify that in a promise, there is an expectation being promised, and that an expectation is a proposition (proposition is defined as in the SEP, here).

• There are agents. 
• Time is discrete and each time unit is called a step.
• At any step, any agent a[1] can make a promise to any other agent a[2]. 
• A promise is a tuple (a[1], a[2], e) where a[1] is the agent that promises to agent a[2]  that expectation e will be satisfied; in a promise, an expectation e is a proposition.
• When a promise is made, the promise is in state Open.
• At a step, if a[2] says that e is satisfied, then the promise is in state Fulfilled.
• At a step, if a[2] says that e is not satisfied, then the promise is in state Broken.
• At any step, the Reputation of an agent is a function of all promises that agent made and the states of these promises.

We then added the following rules to Framework 1 to create Framework 3. Except for one, all rules below are the same as in Framework 2.

• Every agent starts at the first step with zero utility points and zero reputation points.
• Every agent a[i] has a random number n of expectations given by the set E(a[i]) = { e(a[i])[1], …,  e(a[i])[n] }. 
• Every expectation e(a[i])[k] of agent a[i] has a utility of u(e(a[i])[k]) utility points for that agent.
• For any promise (a[i], a[j], e), if the promise is Fulfilled, then the utility of a[j] is increased by u(e(a[j])[k]) utility points and the reputation of a[i] is increased by 1 * u(e(a[j])[k]) reputation points.
• Only the following rule is different from Framework 2: The probability that a promise is Fulfilled is equal to the sum of (i) the reputation of the agent who made the promise, divided by the reputation of the agent who has the highest reputation among all agents, and (ii) the inverse of the utility associated with the expectation in that promise. The probability is capped at 1 if the said sum is higher than 1.
• Expectations and utilities of expectations are public: all agents know all agents’ expectations, and the utility associated with each expectation.
• At every step, an agent chooses to make at most one promise.
• At every step, an expectation appears in at most one promise.
• At every step, a promise is made by at most one agent.
• If a promise is Fulfilled at a step, then no promise made at a subsequent step can be made for the same expectation.
• Every agent aims to maximize their reputation.

The intent with the changed rule (in bold above) is to explore what happens if the probability of a promise being fulfilled positively correlates with the relative reputation of the agent who makes the promise. This captures the intuitive idea that we may want to get promises from the agents who have the highest reputation.

1. Agents and Time

• Let A = {a[1], a[2], …, a[n]} be a finite, non-empty set of agents.
• Time is discrete and ordered as T = {0, 1, 2, …}, where each t in T is a step.

2. Expectations and Utilities

• Each agent a[i] in A has a publicly known, finite set of expectations:
  E(a[i]) = {e(a[i])[1], e(a[i])[2], …, e(a[i])[n[i]]}
• Each expectation e(a[i])[k] is a proposition.
• Each expectation e(a[i])[k] has an associated utility value:
  u(e(a[i])[k]) ∈ ℕ, where 1 ≤ u(e(a[i])[k]) ≤ U_max
• Both expectations and their utility values are public information.

3. Promises

• A promise is a tuple (a[1], a[2], e), where:
• a[1] is the promisor (the agent making the promise),
• a[2] is the promisee (the agent to whom the promise is made),
• e ∈ E(a[2]) is an expectation of the promisee.
• When a promise is created at step t, it is in state Open:
  state[p, t] = Open
• At a later step t’, the promisee evaluates whether the expectation has been satisfied:
• If satisfied: state[p, t’] = Fulfilled
• If not satisfied: state[p, t’] = Broken
• Once Fulfilled or Broken, the state of the promise is permanent.

4. Agent Objectives and Initialization

• Each agent a[i] starts with:
• Utility: U[a[i], 0] = 0
• Reputation: R[a[i], 0] = 0
• Each agent aims to maximize their own reputation R[a[i], t] over time.

5. Utility and Reputation Updates

Let a promise p = (a[i], a[j], e(a[j])[k]).

• If p is Fulfilled at step t, then:
  • U[a[j], t] = U[a[j], t−1] + u(e(a[j])[k])
  • R[a[i], t] = R[a[i], t−1] + u(e(a[j])[k])
• If p is Broken, there are no changes to reputation or utility.

6. Probability of Fulfillment

Let:

• R_max(t) be the maximum reputation among all agents at step t.
• u(e) be the utility value of expectation e in promise p = (a[i], a[j], e).

Then the probability that p is Fulfilled at step t is:

Pr(Fulfilled | p, t) = min[1, (R[a[i], t] / R_max(t)) + (1 / u(e))]

• If R_max(t) = 0, then (R[a[i], t] / R_max(t)) is defined as 0.
• This function combines reputational credibility and task difficulty (via utility).
• The total probability is capped at 1.

7. Constraints

At every step t, the following constraints hold:

1. At most one promise can be made by each agent.
2. Each expectation appears in at most one promise.
3. Each promise is made by only one agent.
4. No promise is made for an expectation that has already been Fulfilled in any previous step.

8. Definitions

• Agent: A decision-making entity capable of issuing and receiving promises.
• Expectation: A publicly known proposition, specific to an agent, associated with a utility.
• Utility: The gain received by an agent when one of its expectations is fulfilled.
• Reputation: A cumulative value reflecting how reliably an agent fulfills others’ expectations.
• Promise: A contractual commitment by one agent to fulfill an expectation of another.
• State: A promise is in one of three states: Open, Fulfilled, or Broken.

A Simple Simulation

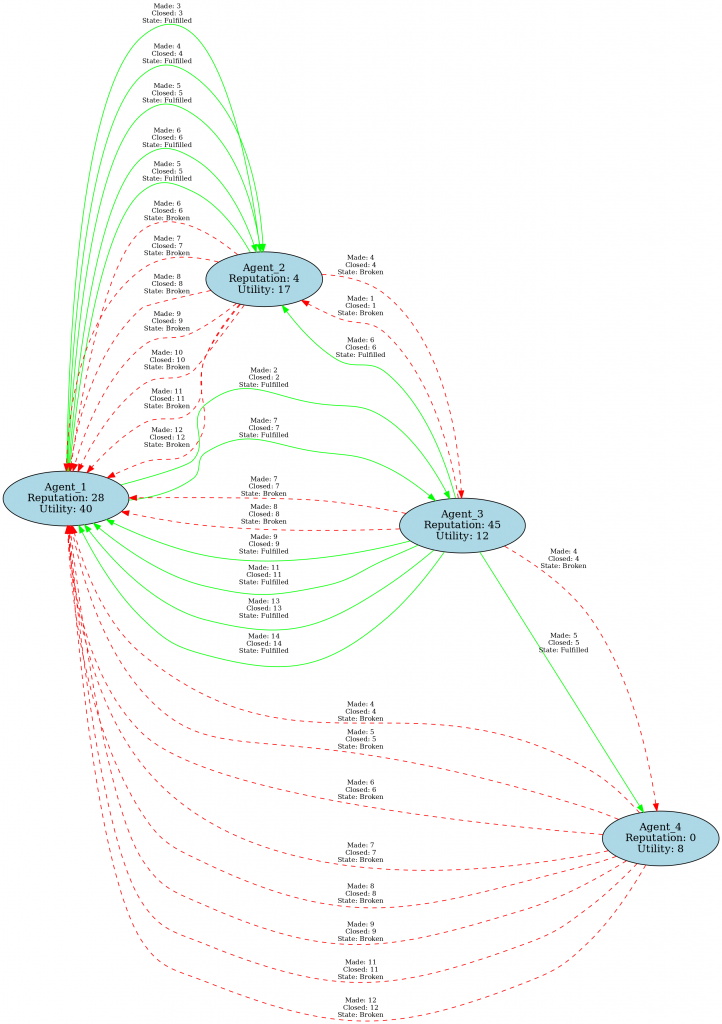
Let’s say we have 4 agents and the simulation runs for 50 steps. Each agent has a random set of expectations in the range of 1 to 5. Utility of an expectation ranges from 1 to 10. The resulting network is shown below, where nodes are agents and links are promises, labeled by the state of the step at which the promise was made, the step at which the promise was closed and the state of the promise. Reputation is calculated as the proportion of fulfilled promises to all promises made by the agent.

Further Reading

• Castelfranchi, C., & Falcone, R. (2010). Trust Theory: A Socio-Cognitive and Computational Model. Wiley.
• Conte, R., & Paolucci, M. (2002). Reputation in Artificial Societies: Social Beliefs for Social Order. Kluwer.
• Kreps, D. M. (1990). Corporate Culture and Economic Theory. In Perspectives on Positive Political Economy.