Drawing Attention to Known vs Unknown Goals

If we need to design governance that influences attention, then it matters if we know or not the goal of the decision maker. This text provides a simple simulation that illustrates the differences between the time it takes for the decision maker to reach the goal in both cases, all else being equal.

This text is part of the series on the design of decision governance. Decision Governance refers to values, principles, practices designed to improve the quality of decisions. Find all texts on decision governance here, including “What is Decision Governance?” here.

If the designer knows the goal that the decision maker is pursuing, the problem consists of designing rules which steer the decision maker towards the known goal. This was illustrated already in the Governance of attention case, in another text, here.

What if the designer does not know the decision maker’s goal? The general idea is that governance should involve a feedback loop that helps the decision maker in their search. This can work as follows. 

1. Governance includes a hypothesis about what the goal may be, or what characteristics it has in case the designer does not want to guess the exact goal. 
2. Governance includes a procedure to steer the decision maker’s attention towards the hypothesized goal, in the cheapest and/or fastest way to determine if that is in fact the goal.
3. If the result of step 2 is that the goal is reached, that’s it, the search stops; if not, then governance needs to include a procedure that sets a new hypothesis about what the goal is, and initiates a new search.

As in other texts with simulations, here, let’s start with a simple known search space represented as a grid, and say that the decision maker starts from the upper left corner.

If we are designing governance and don’t know the goal cell, then we can assume something about it and steer the agent’s search accordingly. For example, we might assume one of the following.

1. The goal is far away from the start, and the rule is to search from the outside in, across the search space.
2. We don’t know anything about where the goal may be, but we know that it will be found if every position in the search space is visited, and to minimize time required to find the goal, the decision maker should not revisit positions (this influences the path to direct the agent onto).
3. We split the search space into some number of parts, select a part, fully explore that, then move to the next, and so on, until all positions in all parts are explored, or the goal is found.

Let’s take the third assumption, that the search space has parts. The governance framework is as follows:

1. The grid (search space) is divided into 4 parts, obtained by dividing the grid in half horizontally and vertically. 
2. Label each part of the grid with a number from 1 to 4. 
3. Randomly order the labels of grid parts.
4. In the given order of grid parts, draw the agent’s attention to move to the first cell of the grid part, which is the upper left corner cell of the grid part. 
5. Once the agent is in the first cell of the grid part, direct the agent’s attention so it traverses all cells in the grid part, without revisiting a cell. 
6. If the agent reached the goal cell, stop. If the agent traversed all cells in the grid part and did not reach the goal cell, then direct the agent to move to the first cell of the next grid part.

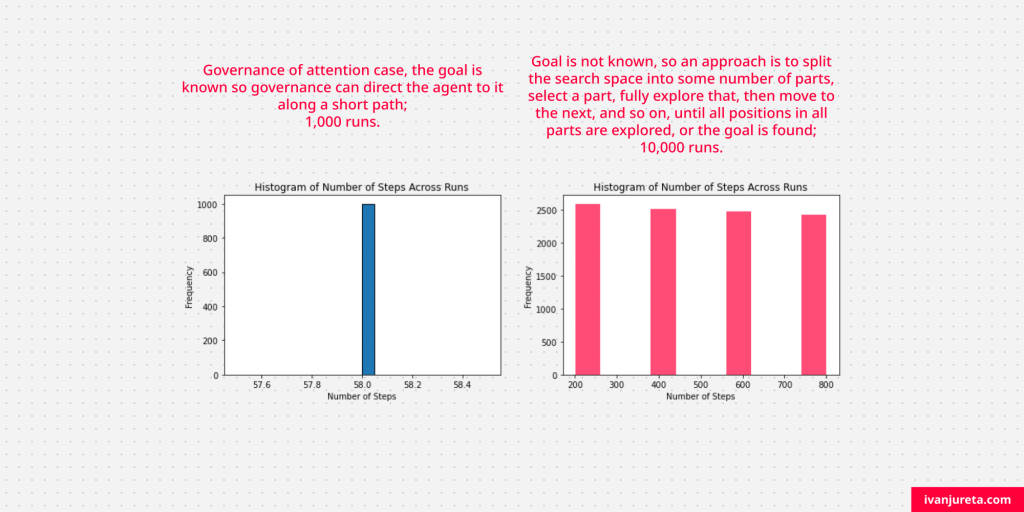
Below are histograms of numbers of steps across 1,000 and 10,000 runs for the case when attention is drawn to the known goal, and when the goal is not known. The difference is obvious.

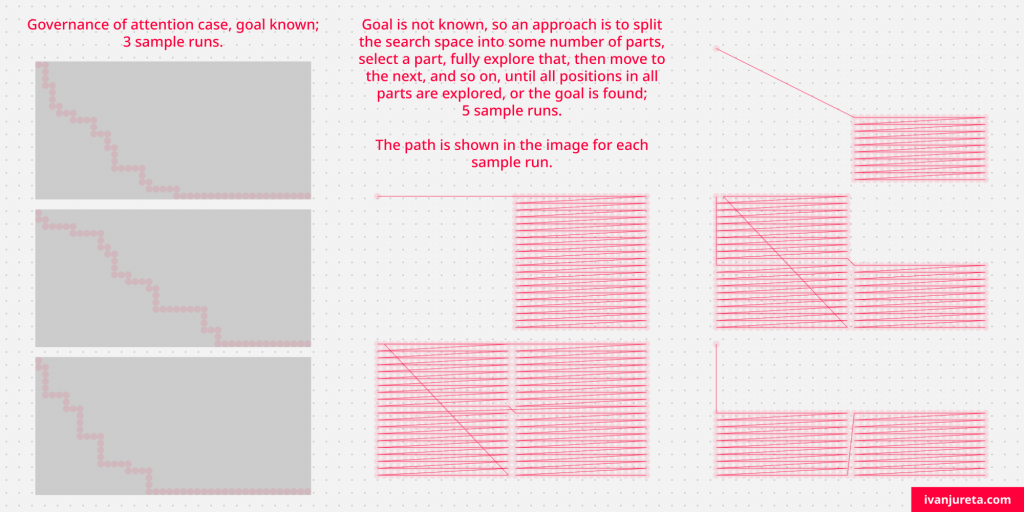
The image below shows sample runs for each of the two cases. In an image, if an agent visited the cell, then a circle is drawn in the cell, and the more times the agent visited that cell, the less transparent the color of the circle. For the case when the goal is not known, the path is also shown.

Code for simulations is available at github, here.

Decision Governance

This text is part of the series on the design of decision governance. Other texts on the same topic are linked below. This list expands as I add more texts on decision governance.

Introduction to Decision Governance

1. What is Decision Governance?
2. What Is a High Quality Decision?
3. When is Decision Governance Needed?
4. When is Decision Governance Valuable?
5. How Much Decision Governance Is Enough?
6. Are Easy Options the Likely Choice?
7. Can Decision Governance Be a Source of Competitive Advantage?

Stakeholders of Decision Governance 

1. Who Is Responsible for Decision Governance in a Firm?
2. Who are the Stakeholders of Decision Governance?
3. What Interests Do Stakeholders Have in Decision Governance?
4. What the Organizational Chart Says about Decision Governance

Foundations of Decision Governance

1. How to Spot Decisions in the Wild?
2. When Is It Useful to Reify Decisions?
3. Decision Governance Is Interdisciplinary
4. Individual Decision-Making: Common Models in Economics
5. Group Decision-Making: Common Models in Economics
6. Individual Decision-Making: Common Models in Psychology
7. Group Decision-Making: Common Models in Organizational Theory

Role of Explanations in the Design of Decision Governance

1. Explaining Decisions
2. Simple & Intuitive Models of Decision Explanations
3. Max(Utility) from Variety & Taste
4. Expected Uncertainty to Unexpected Utility
5. Perceptiveness & Experience Shape Rapid Choices

Design of Decision Governance

1. The Design Space for Decision Governance
2. Decision Governance Concepts: Situations, Actions, Commitments and Decisions
3. Decision Governance Concepts: Outcomes to Explanations
4. Slow & Complex Decision Governance and Its Consequences

Design Parameters of Decision Governance

Design parameters of decision governance, or factors that influence decision making and that we can influence through decision governance:

• Factors influencing how an individual selects and processes information
• Factors influencing information the individual can gain access to

Factors influencing how an individual selects and processes information in a decision situation, including which information the individual seeks and selects to use:

1. Psychological factors, which are determined by the individual, including their reaction to other factors:
   1. Attention:
      • Attention Depends on Stimuli & Goals
      • Motivated Reasoning: How To Detect And Mitigate Its Risks
   2. Memory:
      • Selective Memory Can Be Desirable
   3. Mood
   4. Emotions:
      • Emotions Mediate Decisions Always and Everywhere
   5. Temporal Distance:
      • Why Perception of Long Term Outcomes Should Be Influenced First?
   6. Social Distance:
      • Increased Social Distance (Over)Simplifies Explanations
   7. Expectations
   8. Uncertainty
   9. Attitude
   10. Values
   11. Goals:
       • Goals: How Goals Shape Decisions
       • Goals: How Goals Form and Change
       • Goals: Factors That Stabilize and Destabilize Goals
       • Goals: Factors Influencing Goal Selection
       • Goals: How to Improve Alignment to a Team Goal
   12. Preferences
   13. Competence
2. Social factors, which are determined by relationships with others:
   1. Impressions Of Others: How They Influence Decisions And How To Regulate Them
   2. Reputation
   3. Social Hierarchies:
      • Social Hierarchies: Why They Matter for Decision Governance
      • Social Hierarchies: Benefits and Limitations in Decision Processes
      • Social Hierarchies: How They Form and Change 
      • Power: Influence on Decision Making and Its Risks
      • Power: Relationship to Psychological Factors in Decision Making
      • Power: Sources of Legitimacy and Implications for Decision Authority
      • Power: Stability and Destabilization of Legitimacy

Factors influencing information the individual can gain access to in a decision situation, and the perception of possible actions the individual can take, and how they can perform these actions:

• Governance factors, which are rules applicable in the given decision situation:
  1. Incentives
     • Incentives: Components of Incentive Mechanisms
     • Incentives: Example of a Common Incentive Mechanism
     • Incentives: Building Out An Incentive Mechanism From Scratch
  2. Rules
     • Rules-in-use
     • Rules-in-form
  3. Institutions
• Technological factors, or tools which influence how information is represented and accessed, among others, and how communication can be done
• Environmental factors, or the physical environment, humans and other organisms that the individual must and can interact with
  1. Detail: Level of Detail Can Influence Probability Estimates

Change of Decision Governance

1. Public Policy and Decision Governance:
   • What is the Role of Public Policy in Decision Governance?
   • Dynamics of Public Policy Development
   • How Does Public Policy Influence Decision-Making?
2. Compliance to Policies:
   • Adapting a Decision Process to Comply with a Policy
   • How a Decision Process Can Create Evidence of Compliance
3. Transformation of Decision Governance
   • Punctuated Equilibrium: How to know if a Decision Process is ready for disruption
   • Policy Windows: What They Are And When They Occur
4. Mechanisms for the Change of Decision Governance
   • Incrementalism: What it is, and when/how to implement it in decision governance
   • Governance Dynamics: Change Driven by Cases and Principles
   • Governance Dynamics: Case-Based Development of Decision Governance