Incentives: Building An Incentive Mechanism From Scratch

This is a case study in the series on incentives in decision governance. Let’s assume that we need an incentive mechanism to stimulate employee performance by allocating bonuses based on peer opinion. The mechanism should work as follows:

• During a quarter, employees work on various tasks and projects together, and when an employee A believes that another employee B has done a good work, A can add one point to the performance score of B.
• Employees cannot give points to themselves.
• The share of the bonus budget that an employee receives is proportional to the share of that employee’s points in the total points assigned over the quarter to all employees.

Let’s make a first version of it, and then see what the pros and cons may be, and adjust accordingly.

This text is part of the series on the design of decision governance. Decision Governance refers to values, principles, practices designed to improve the quality of decisions. Find all texts on decision governance here, including “What is Decision Governance?” here.

Basic Mechanism

This incentive mechanism can be described mathematically as follows:

1. \( N \): Total number of employees.
2. \( B \): Total bonus budget available for distribution.
3. \( p_{ij} \): Points given by employee \( i \) to employee \( j \) during the quarter (\( p_{ij} \geq 0 \) and \( p_{ii} = 0 \) since employees cannot give points to themselves).
4. \( P_j \): Total points received by employee \( j \), calculated as: \(P_j = \sum_{i=1}^{N} p_{ij}, \quad \forall j \in {1, \dots, N}.\)
5. \( P_{\text{total}} \): Total points assigned across all employees during the quarter: \( P_{\text{total}} = \sum_{j=1}^{N} P_j = \sum_{j=1}^{N} \sum_{i=1}^{N} p_{ij}. \)
6. \( s_j \): Share of the total points received by employee \( j \), calculated as: \(s_j = \frac{P_j}{P_{\text{total}}}, \quad \text{if } P_{\text{total}} > 0.\)
7. \( b_j \): Bonus allocated to employee \( j \), calculated as: \( b_j = s_j \cdot B = \frac{P_j}{P_{\text{total}}} \cdot B, \quad \text{if } P_{\text{total}} > 0.\)

Note the following:

• If \( P_{\text{total}} = 0 \) (i.e., no points are assigned during the quarter), \( b_j = 0 \) for all \( j \), as there are no contributions to distribute.
• The mechanism ensures that the bonuses are distributed proportionally to the points received by each employee relative to the total points assigned.
• We can have a budget constraint: The total bonuses distributed equal the bonus budget \( B \): \( \sum_{j=1}^{N} b_j = B. \)
• Employees’ bonuses depend solely on their peers’ evaluations, reflecting the collective perception of their contributions.
• This mechanism incentivizes employees to recognize and reward the contributions of their peers while maintaining a fixed budget for bonuses.

Benefits of the Incentive Mechanism

1. Encourages Collaboration: By relying on peer evaluations, the mechanism incentivizes employees to work effectively with others and contribute to team success, fostering a collaborative workplace culture.
2. Recognizes Informal Contributions: Employees often notice valuable efforts and contributions that might not be apparent to managers. This mechanism captures such informal contributions, leading to a more comprehensive assessment.
3. Promotes Continuous Feedback: Employees are encouraged to pay attention to and acknowledge their colleagues’ work, creating a culture of regular and constructive feedback.
4. Dynamic and Flexible: The system adapts to changing contributions within each quarter. Employees are motivated to sustain high performance over time rather than relying on past achievements.
5. Aligns with Team Objectives: As bonuses depend on peer recognition, employees are likely to align their efforts with team goals to receive acknowledgment and points from others.
6. Transparency in Bonus Allocation: Since bonuses are directly proportional to peer-assigned points, the process is transparent and avoids managerial bias, increasing perceived fairness.

Risks of the Incentive Mechanism

1. Risk of Collusion: Employees might form alliances to exchange points or allocate them preferentially among friends or sub-groups, undermining the fairness of the system.
2. Popularity Over Merit: High-performing but less socially engaged employees might be overlooked, while more sociable employees may receive disproportionate rewards.
3. Manipulation and Strategic Behavior: Employees might strategically withhold points or assign them based on factors unrelated to performance, such as personal favors or expectations of reciprocity.
4. Demotivation and Resentment: If employees perceive the system as unfair or prone to favoritism, it could lead to resentment and demotivation, harming morale and productivity.
5. Administrative Burden: Tracking and managing peer-assigned points could require significant effort, particularly in larger organizations or those with complex reporting structures.
6. Short-Term Focus: Employees may prioritize visible, immediate contributions that earn peer recognition over longer-term, less noticeable tasks essential to organizational success.
7. Potential for Exclusion: New or marginalized employees might struggle to integrate into the social network and may receive fewer points, leading to unequal opportunities.

Mitigation Strategies

To address these risks, the organization could:

• Set Guidelines: Clearly define criteria for assigning points to ensure they reflect meaningful contributions.
• Monitor Patterns: Regularly review point distributions to identify anomalies, such as collusion or bias.
• Provide Anonymity: Allow employees to assign points anonymously to reduce fear of retaliation or bias.
• Combine with Other Metrics: Use this mechanism as one component of a broader performance evaluation system, incorporating manager reviews and objective performance metrics.
• Educate Employees: Offer training on the purpose and ethical use of the system to promote responsible participation.

Mitigating the Risk of Collusion

To minimize the risk of collusion in the proposed incentive mechanism, the model can be improved by introducing additional constraints, checks, and features that discourage strategic manipulation and ensure fair allocation of points. Here are several approaches:

1. Implement Normalization of Points

Adjust the influence of each employee’s points based on their distribution behavior. For example:

• Cap the points given by any employee \( i \): \( \sum_{j=1}^{N} p_{ij} \leq C, \) where \( C \) is a fixed maximum, ensuring no single employee can disproportionately influence the total.
• Weight Points Based on Consistency: Use statistical techniques to detect unusually biased distributions (e.g., giving all points to one or a few individuals). These could be flagged and adjusted or excluded.

2. Introduce Anonymity in Voting

• Make point assignments anonymous to reduce social pressures or reciprocal behaviors.
• Anonymity reduces the likelihood of employees forming explicit agreements to exchange points.

3. Require Justifications for Points

• Employees must provide brief justifications for why they assign points to others. These justifications can be reviewed periodically to ensure alignment with performance objectives.
• The process adds accountability, discouraging arbitrary or collusive behavior.

4. Use Statistical Detection of Collusion

• Apply machine learning or statistical methods to detect collusive behavior. For example:
• Clustering of points: Repeated mutual exchanges among a subset of employees could indicate collusion.
• Variance checks: Unusually consistent scoring patterns between certain employees may flag unfair practices.
• Identified cases could trigger audits or penalties.

5. Introduce Diversity in Evaluators

• Weight the points based on the diversity of evaluators. Contributions recognized by a larger and more diverse group of peers carry more weight than points concentrated from a few colleagues.
• For instance, define a diversity factor \( d_j \) for each employee \( j \), calculated as: \( d_j = \text{Number of distinct employees giving points to } j. \) The final score could then be weighted as: \( \text{Adjusted points for } j = P_j \cdot f(d_j), \) where \( f(d_j) \) is a monotonically increasing function of \( d_j \).

6. Mix Peer and Managerial Assessments

• Introduce a managerial review component to validate or adjust the distribution of points. For example: \( \text{Final points for } j = \alpha \cdot P_j + (1 – \alpha) \cdot M_j, \) where \( M_j \) is the manager-assigned score, and \( \alpha \) is a weighting factor (e.g., \( \alpha = 0.7 \)).

7. Penalize Disproportionate Behaviors

• Penalize employees who overly concentrate their points on a single individual. For example, if \( p_{ij} \) exceeds a set threshold, only a fraction of those points are counted: \( \text{Effective } p_{ij} = \min(p_{ij}, T), \) where \( T \) is the maximum permissible allocation to any single individual.

8. Allow Points Redistribution

• Introduce a mechanism for unused or excessively concentrated points to be redistributed proportionally among other employees. For instance: If \( \sum_{j=1}^{N} p_{ij} < C \), the remaining budget can be redistributed to employees \( j \) based on predetermined criteria (e.g., task contributions or workload).

9. Encourage Objective Criteria for Points

• Predefine clear, measurable performance metrics tied to tasks, such as meeting deadlines, quality of work, or team contribution.
• Employees are encouraged to allocate points only for contributions aligned with these metrics, reducing subjective bias.

10. Periodic Rotation of Peer Groups

• For larger teams, employees can be rotated into smaller, temporary groups each quarter. Points are then assigned within these groups only, making collusion across the organization more challenging.

Improved Mechanism with Diversity and Managerial Adjustment

An improved formula could integrate these enhancements as follows:

\( b_j = \frac{(\alpha \cdot P_j \cdot f(d_j)) + ((1-\alpha) \cdot M_j)}{\sum_{k=1}^{N} \left[(\alpha \cdot P_k \cdot f(d_k)) + ((1-\alpha) \cdot M_k)\right]} \cdot B. \)

Where:

• \( f(d_j) \): Diversity weight for employee \( j \).
• \( M_j \): Managerial evaluation for employee \( j \).
• \( \alpha \): Weighting factor for peer-assigned vs. managerial evaluations.

Fixing the Number of Points Each Employee Can Allocate

If every employee is restricted to allocate a fixed number of points (\(C\)), the model changes as follows:

Revised Assumptions and Notation

1. \( C \): The fixed number of points each employee can allocate in a quarter.
2. \( p_{ij} \): Points given by employee \( i \) to employee \( j \), subject to: \( \sum_{j=1}^{N} p_{ij} = C, \quad p_{ij} \geq 0, \quad p_{ii} = 0. \)
3. \( P_j \): Total points received by employee \( j \), calculated as: \( P_j = \sum_{i=1}^{N} p_{ij}. \)
4. \( P_{\text{total}} \): Total points assigned across all employees: \( P_{\text{total}} = \sum_{j=1}^{N} P_j = N \cdot C. \) Since each of the \( N \) employees allocates \( C \) points, the total points \( P_{\text{total}} \) is constant.
5. \( s_j \): Share of total points received by employee \( j \), calculated as: \( s_j = \frac{P_j}{P_{\text{total}}}. \)
6. \( b_j \): Bonus allocated to employee \( j \), proportional to \( s_j \), calculated as: \( b_j = s_j \cdot B = \frac{P_j}{P_{\text{total}}} \cdot B.\)

Key Changes in the Mechanism

1. Point Allocation Constraint: The restriction \( \sum_{j=1}^{N} p_{ij} = C \) ensures that all employees contribute equally to the total pool of points. This eliminates situations where some employees give more or fewer points, leading to uniform participation.
2. Fixed Total Points: With \( P_{\text{total}} = N \cdot C \), the denominator in the bonus formula becomes constant, simplifying calculations and ensuring that fluctuations in the total number of points are no longer a factor.
3. Uniform Voting Power: Since every employee has the same number of points to allocate, their influence on the bonus distribution is equalized, reducing disparities caused by differences in voting behavior.

Revised Formula for Bonuses

The bonus for employee \( j \) becomes: \( b_j = \frac{P_j}{N \cdot C} \cdot B. \), where:

• \( P_j = \sum_{i=1}^{N} p_{ij} \),
• \( N \cdot C \) is the fixed total number of points available in the system.

Benefits of This Modification

1. Reduces Collusion Risk: Employees cannot manipulate the system by allocating disproportionate points to specific individuals because the total points they can allocate are capped.
2. Encourages Thoughtful Allocation: Employees must carefully decide how to distribute their limited points, prioritizing those they believe contribute most effectively.
3. Simplifies Administration: The fixed total points make calculations straightforward and eliminate fluctuations in \( P_{\text{total}} \), ensuring a stable basis for bonus distribution.

Implications

While this modification reduces collusion and adds fairness, it may still face risks such as:

• Popularity bias: Employees may allocate points based on personal relationships rather than merit.
• Undervaluation of certain contributions: Employees performing critical but less visible tasks may receive fewer points.

These risks can be addressed by introducing mechanisms such as:

• Anonymity in point allocation.
• Guidelines or criteria for point allocation.
• Managerial oversight or adjustment for points.

Simulation

Assume a firm has 1000 employees. Each employee is allocated 5 points to distribute in a quarter. Assume that in a quarter, an employee collaborates with a random number of employees, where that number is between 5 and 25 employees. Assume that the informal network in the company resembles in its structure a typical social network. Assume that any employee prefers to give points to employees who are closer to them in their informal network. What would the histogram of points assigned to each employee look like?

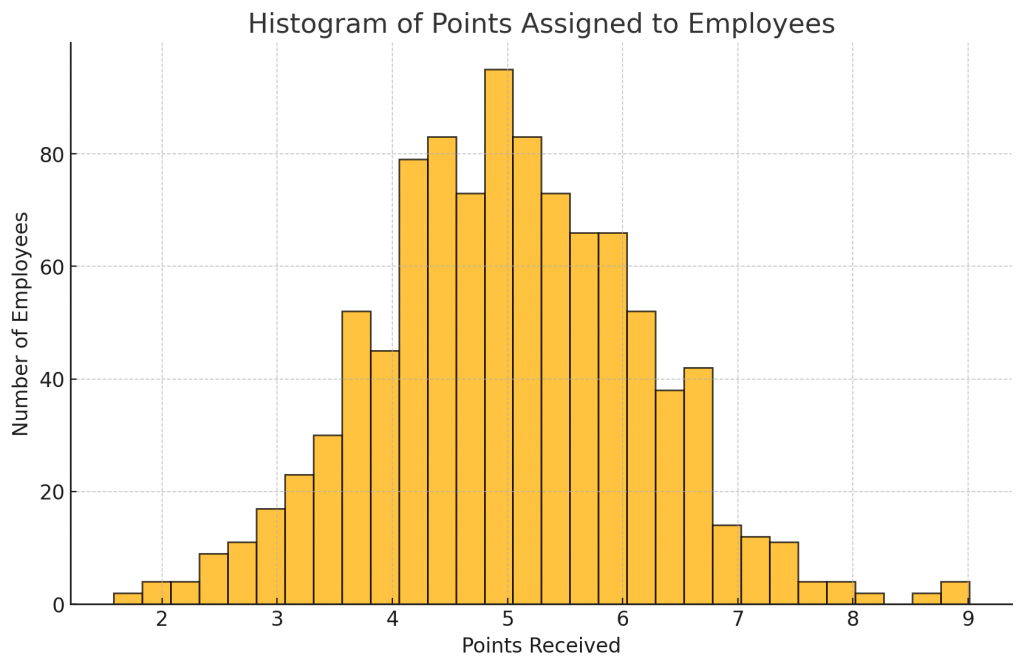
The histogram above represents the distribution of points received by employees under the given assumptions. The shape of the histogram reflects the uneven distribution of points, influenced by the structure of the informal network and the preference for assigning points to closer connections within that network. Employees with a higher centrality in the network tend to receive more points. ​

Impact of the Structure of the Informal/Social Network Within the Firm

In the context of social or informal networks, centrality refers to the importance or prominence of an employee within the network. There are several types of centrality measures, each capturing a different aspect of importance:

Types of Centrality

1. Degree Centrality:
   • Measures the number of direct connections an employee has. In this context, it indicates how many other employees a person collaborates with.
   • Employees with high degree centrality are often more active in collaboration and are likely to receive more points because they interact with more colleagues.
2. Betweenness Centrality:
   • Measures the extent to which an employee lies on the shortest paths between other employees.
   • Employees with high betweenness centrality act as bridges or intermediaries, connecting different groups within the network. Their contributions are often critical in facilitating communication and collaboration.
3. Closeness Centrality:
   • Measures how close an employee is to all other employees in terms of the shortest paths. It reflects how quickly an employee can reach others in the network.
   • Employees with high closeness centrality are likely to receive more points because they can collaborate effectively across the organization.
4. Eigenvector Centrality:
   • Measures how well-connected an employee is to other well-connected employees. It captures influence within the network.
   • Employees with high eigenvector centrality are often key influencers or hubs within the network, making them more likely to receive recognition.

Implications of High Centrality

An employee with higher centrality is more likely to:

• Be visible to others in the network, leading to more recognition of their contributions.
• Be involved in multiple collaborations, which increases their likelihood of receiving points from colleagues.
• Serve as a key resource or connector, further increasing their influence and perceived value.

In the context of the incentive mechanism, employees with higher centrality (especially degree or eigenvector centrality) are more likely to receive a larger share of points, skewing the distribution in their favor. This highlights the role of network structure in shaping outcomes under the point allocation system. It also shows an important risk with this incentive mechanism.

Parameters Shaping the Distribution of Points

In the simulated situation, the distribution of points among employees is influenced by several parameters related to the structure of the informal network, the point allocation process, and the characteristics of employee collaboration. Here’s a breakdown of the key factors:

1. Network Parameters

These parameters define the structure of the informal network and directly affect how employees interact:

• Network Type (e.g., Small-World, Scale-Free, Random): Different network structures distribute connections differently. For example:
  • A small-world network has clusters of tightly connected nodes, leading to some employees being more central.
  • A scale-free network produces a few highly connected nodes (hubs), creating a long tail in the distribution of points.
  • A random network spreads connections more evenly, leading to a more uniform distribution of points.
• Average Degree of the Network \( k \):
• The average number of direct connections per employee influences how widely points are distributed.
• Higher \( k \) results in more potential collaborators for each employee, reducing point concentration on a few individuals.
• Rewiring Probability \( p \)) in Small-World Networks:
• Affects the balance between local clusters and long-distance connections.
• Higher \( p \) increases randomness, creating more global connections and spreading points more evenly.

2. Employee Collaboration Parameters

These parameters influence how employees interact within the network:

• Range of Collaborators per Employee:
• The minimum \( \text{min_collaborators} \) and maximum \( \text{max_collaborators} \) determine the variability in the number of colleagues each employee interacts with.
• Wider ranges increase variation in the distribution, while tighter ranges make the distribution more uniform.
• Preference for Close Connections:
• If employees prefer to allocate points to those closer to them in the network (e.g., direct neighbors), points concentrate on central or well-connected employees.
• Reducing this preference (e.g., randomizing point allocation) leads to a more even distribution.

3. Point Allocation Parameters

These parameters control the mechanics of distributing points:

• Points Per Employee \( C \): Higher \( C \) increases the total number of points distributed and can smooth the distribution, as employees have more flexibility in allocation.
• Point Allocation Strategy: Equal allocation to all collaborators versus proportional allocation based on collaboration intensity or network proximity affects the spread of points.

4. Bonus-Specific Parameters

Although not directly simulated in the network, these affect the interpretation of the distribution:

• Normalization or Weighting Schemes: Adjustments for diversity of allocators, quality of contributions, or fairness considerations can shape the distribution indirectly.

5. Stochastic Effects

Randomness in the simulation influences the exact shape of the distribution:

• Random Assignment of Collaborators: Variability in who collaborates with whom introduces noise, especially in smaller networks or when collaboration ranges are wide.
• Variability in Network Initialization: Each instantiation of the network (e.g., small-world with rewiring) can result in a slightly different topology, affecting point distribution.

Impact of These Parameters on the Distribution Shape

1. Highly Connected Hubs (Scale-Free Networks): Skewed distributions with a long tail, where a few employees receive disproportionately high points.
2. High Clustering (Small-World Networks): Bimodal or multi-modal distributions, where employees in dense clusters receive more points than isolated individuals.
3. Uniform Collaboration (Random Networks): Bell-shaped or uniform distributions, depending on the range of collaborators and allocation strategy.

Making the Distribution More Equitable

To make the distribution of points more equitable across employees, several parameters related to the network structure, collaboration dynamics, and point allocation mechanism can be adjusted. Below is an analysis of the parameters to influence and the strategies to achieve greater equity:

Reduce Network Centrality Bias

• Action: Modify the informal network structure to decrease reliance on central or highly connected employees.
• How: Increase the network’s rewiring probability (\(p\)) in small-world networks to create more random, global connections. This reduces the dominance of local clusters and spreads interactions more evenly.
• Result: Employees in peripheral positions gain access to collaborators, reducing concentration of points on central employees.

Increase Average Degree

• Action: Increase the average number of connections per employee.
• How: Expand the neighborhood size (number of direct connections) for each employee.
• Result: Ensures that points are distributed to a broader set of collaborators, reducing the advantage of being a hub.

Broaden Collaboration Range

• Action: Widen the minimum and maximum number of collaborators (\( \text{min_collaborators} \) and \( \text{max_collaborators} \)).
• How: Encourage employees to collaborate with a greater number of peers, possibly through task assignments or project structures.
• Result: Points are less concentrated among a small group of frequent collaborators, promoting equity.

Encourage Diverse Collaborations

• Action: Incentivize employees to collaborate with colleagues outside their immediate network.
• How: Reward cross-departmental projects or randomly assign some collaborations to balance interaction opportunities.
• Result: Reduces the tendency to allocate points within tightly-knit groups.

Cap Points Per Collaborator

• Action: Limit the number of points that can be assigned to any single collaborator.
• How: Introduce a rule such as: \( p_{ij} \leq T, \quad \text{where } T \text{ is a maximum threshold}. \)
• Result: Prevents employees from disproportionately favoring a single colleague, spreading points more evenly.

Introduce a Baseline Allocation

• Action: Distribute a fixed portion of points equally among all employees and allow the remainder to be distributed as per the mechanism.
• How: Allocate a percentage of each employee’s points (\( C \)) equally across all collaborators and reserve the rest for preferential allocation.
• Result: Balances equity (via the baseline) and merit (via the remaining points).

Weight Points Based on Network Diversity

• Action: Reward points given to diverse collaborators more heavily.
• How: Use a diversity weight: \( \text{Effective } p_{ij} = p_{ij} \cdot f(d_j),\) where \( f(d_j) \) is a function that increases with the diversity of \( j \)’s collaborators.
• Result: Encourages points to be distributed more broadly, reducing concentration.

Normalize Received Points

• Action: Adjust the final points received by each employee to account for structural network inequities.
• How: Apply a normalization factor: \( \text{Adjusted Points for } j = \frac{P_j}{\text{Number of Collaborators for } j}. \)
• Result: Ensures employees with fewer collaboration opportunities are not unduly disadvantaged.

Introduce Equalization Mechanisms

• Action: Redistribute excess points from highly recognized employees to those with fewer points.
• How: Apply a cap on the maximum points any employee can receive and redistribute the surplus to others proportionally.
• Result: Limits extreme disparities while maintaining the incentive structure.

Promote Inclusion

• Action: Ensure that all employees have access to collaborative opportunities.
• How: Use project rotations or mentorship programs to integrate isolated employees into key teams.
• Result: Improves collaboration equity, reducing point distribution disparities.

Provide Guidelines for Point Allocation

• Action: Educate employees on fair point allocation criteria.
• How: Encourage employees to assign points based on objective contributions rather than personal relationships or proximity.
• Result: Reduces favoritism and increases perceived fairness.

Expected Effects on Distribution

By implementing these changes, we get the following.

1. Narrower Distribution Spread: Central employees receive fewer points relative to the baseline, while peripheral employees receive more.
2. Increased Mode Frequency: More employees cluster around the average number of points, reducing extremes.
3. Higher Perceived Fairness: Employees are more likely to perceive the system as equitable, enhancing satisfaction and engagement.

These strategies balance merit-based incentives with fairness, ensuring that the distribution of points better reflects both contribution and opportunity.

As you may notice, most changes will generate new risks – this is what makes incentive design so interesting: there’s no best solution.